今天開始介紹多元二次多項式密碼系統！首先我們現來研究最主要的數學物件「多元二次方程組」，並探討如何把這個東西做成密碼系統（雙極構造法）。

多元二次多項式

數學描述

多元二次多項式系統是形如以下的多項式系統：

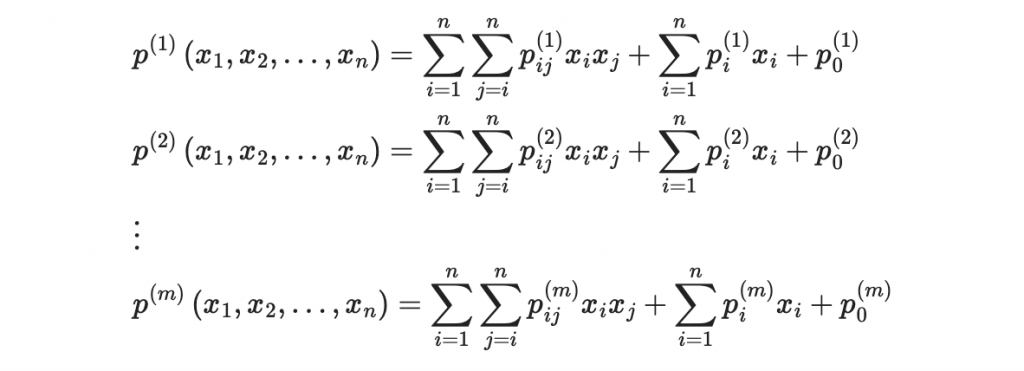
這裡，每個多項式 p^{(k)}(x_1, x_2, \ldots, x_n) 都是變量 x_1, x_2, \ldots, x_n 的二次多項式。每個多項式由二次項、一次項和常數項組成。讓我們來看一個具體的例子

假設我們有兩個變量 x_1 和 x_2，以及兩個多項式 p^{(1)} 和 p^{(2)}，構成的多變量二次多項式系統可以表示如下：

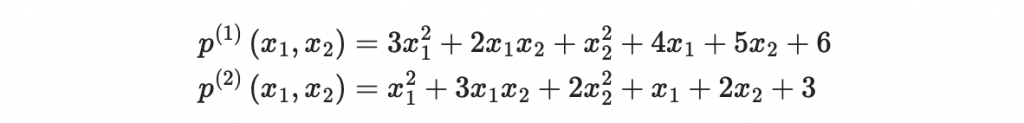
在這個例子中，我們可以看到每個多項式都包含了二次項（如 3x_1^2）、一次項（如 4x_1）和常數項（如 6）。這些多項式可以用來構造多變量加密系統。

困難問題

假設我們把上面這個例子記做 F

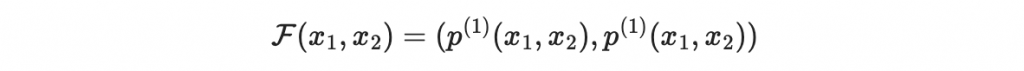
那我們可以很快速的求到函數值

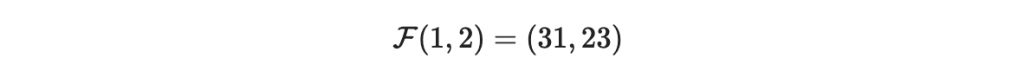
可是如果反過來，要找到某組 (x1, x2) 滿足

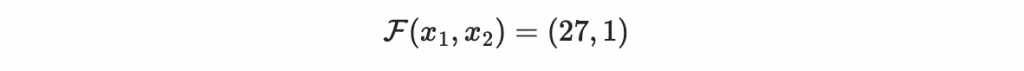
那這個問題是，蠻複雜的（歡迎求到解的朋友在底下留言😀）

因此，對於一個多元二次方程組來說

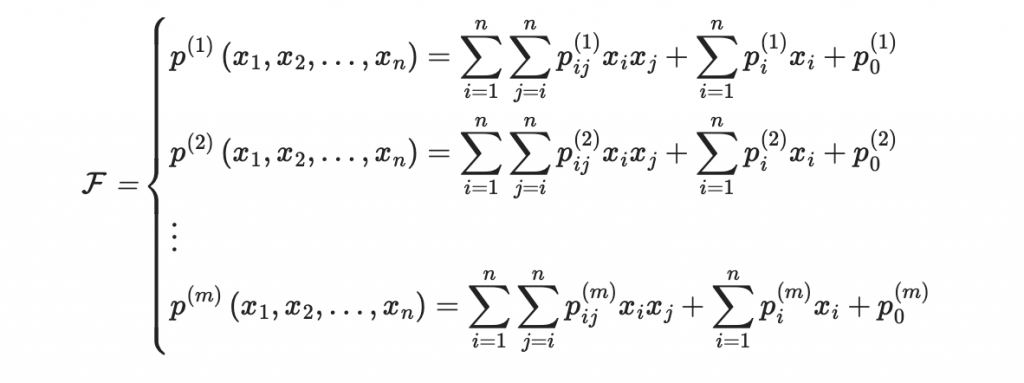
要計算 F 的反函數，是非常困難的。也因為這樣的困難度（hardness）我們可以把它設計成密碼協議

雙極構造法

我們開始來介紹，這樣的數學物件如何被做成密碼協議

線性變換與仿射變換

所謂的線性變換就是用一個矩陣乘上作用的向量，如以下算式

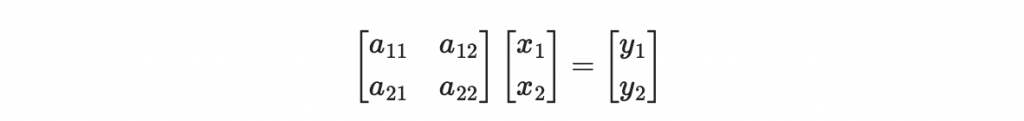
這個算式就是一個對

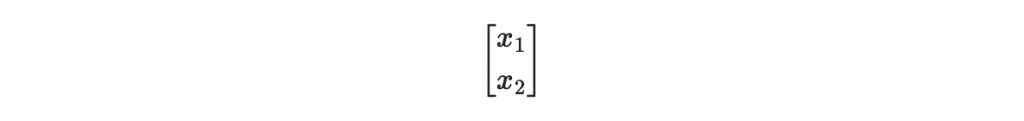
的線性變換。

所謂的仿射變換就是在線性變換之後再加上一個常數向量，如以下算式

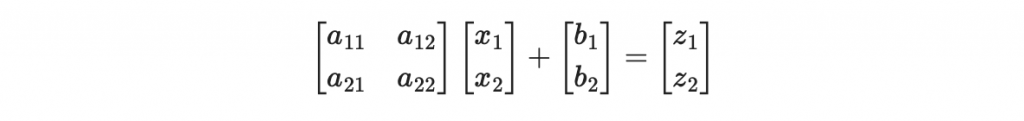
這個算式就是一個對

的仿射變換。

接著，以下這個特殊矩陣無論乘上誰，都不會改變他：

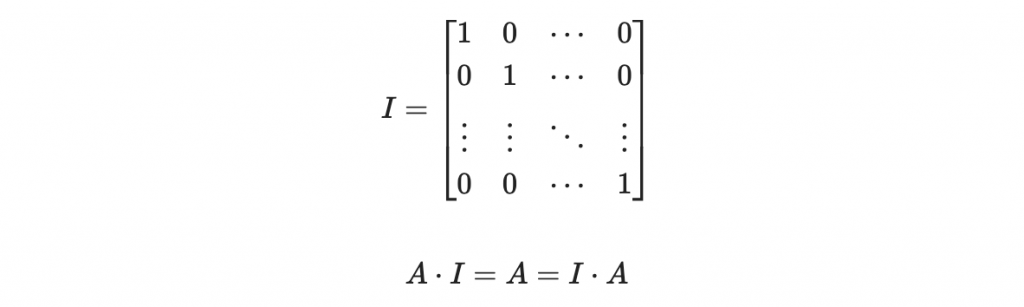
再來，我們說一個矩陣 A 是可逆的，如果他有乘法反元素（又是你乘法反元素），即可以找到一個矩陣 A^-1 ：

雙極構造法

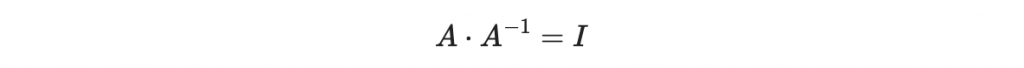
首先我們要生成兩個在 n 維度空間中的可逆的仿射變換：

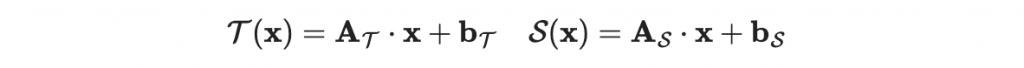
其中我們要求：首先 A_T 與 A_S 都要可逆，其次 T 是 n 維空間上的仿射變換、S 是 m 維空間上的仿射變換。

我們也要生成一個「很好求反函數的」多元二次多項式系統 F ，這裡的「很好求反函數」是雙極構造法中的規定，至於如何生成這樣「很好求反函數的」多元二次多項式，我們會在後面介紹幾種不同的生成方法。

好！我們有一個「很好求反函數的」多元二次多項式系統 F ：

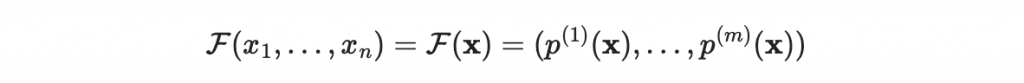
這是一個從 n 維空間到 m 維空間的函數。

我們於是可以把剛剛這三個東西串起來：

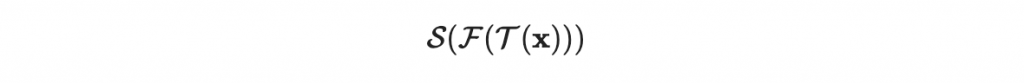
一開始 x 是一個 n 維向量，接著被 T 送到一個 n 維向量，接著被 F 送到 m 維向量，最後被 S 送到一個 m 維向量。

雖然 F 是一個很好求反函數的多元二次多項式，但是經過 S 與 T 的雙面夾擊後（這裡的 S 與 T 都是隨機生成），最後的結果 S(F(T(x)))，仍然是一個多元二次多項式，而且是係數很亂，看起來根本就是隨機生成的多元二次多項式，此時，求反函數的問題就困難許多。

因此，私鑰為 (T, S, F) 三個函數，而公鑰為 S(F(T(x)))，就完成一個公要鑰密碼系統啦！

當我們使用加密模式時，我們把要傳送的訊息做成一個 n 維向量 m，然後計算密文 e = S(F(T(m)))。擁有私鑰的接收者拿到 e 後，根據他手上私鑰的資料，求 S F T 的反函數，於是可以計算出 m 。

takeaway

• 所謂的多元二次多項式是如下形式的函數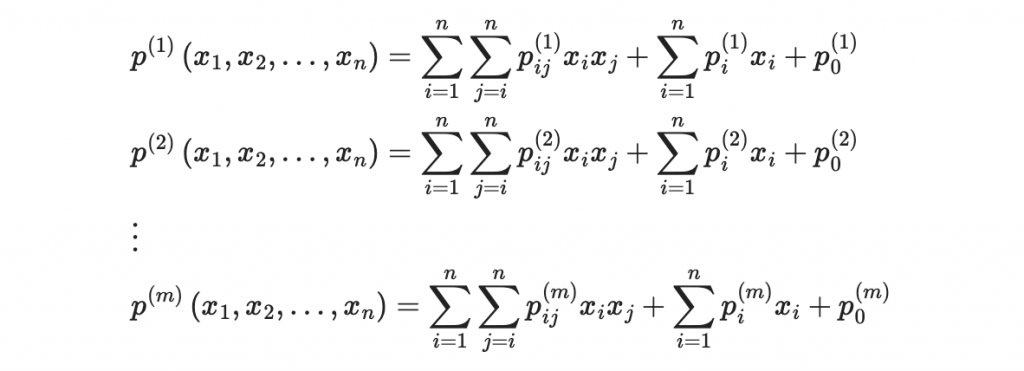
  

• 困難問題：令 F 為一個多元二次多項式，計算正向的函數值很容易，但是計算反函數值通常非常困難

• 雙極構造法是先生成一個很好求反函數的多元二次多項式系統，用兩個隨機的仿射變換把他搞亂，做出一個看起來很像隨機生成的多元二次多項式系統。容易求解的多元二次系統與兩個仿射變換就被當作私鑰、看起來隨機的多元二次多項式系統就被當作公鑰。

ref
DING, Jintai; GOWER, Jason E.; SCHMIDT, Dieter S. Multivariate public key cryptosystems. Springer Science & Business Media, 2006.